Werbung
Die Graham Zahl
Benjamin Grossbaum wurde 1894 in London geboren. Während des zweiten Weltkrieges ließen seine Eltern den Nachnamen in Graham ändern. Er war Wirtschaftswissenschaftler, Dozent und Investor.
Benjamin Graham wird als der „Vater des Value Investings“ bezeichnet. Ihn störte es dass Aktien zunehmend nicht als Unternehmensbeteiligungen sondern als Spekulationsobjekte betrachtet wurden.
Die Graham Zahl ist eine Formel die aus den Aussagen von Benjamin Graham abgeleitet wurde. Laut Graham solle man niemals mehr als das 1,5-fache des Buchwertes oder das 15-fache der Jahresgewinne für ein Unternehmen zahlen.
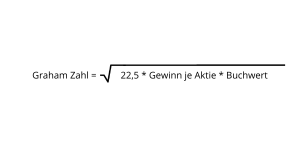
Sie gibt damit den maximalen Kaufpreis für ein Unternehmen an. Dennoch sollte man sie niemals 1 zu 1 verwenden. Es sollten stehts weitere Kennzahlen angesehen werden.
Dann gibt es natürlich auch noch eine Graham Formel die aus dem Buch „Security Analysis“ stammt. Die Formel berücksichtigt, dass Unternehmen, das kein Kurs-Gewinn-Verhältnis von etwa 8,5 aufweisen sollte.
Die Graham Formel wurde später von Benjamin Graham modifiziert, denn die ursprüngliche Formel beinhaltete keine Renditeforderung, die neue Formel lautet also:

Der Faktor 4,4 steht für den risikolosen Zinssatz, der damals bei 4,4 lag während Y für den heutigen risikolosen Zinssatz steht.
Wer jedoch die Graham Formel verwenden will sollte darauf achten dass der Gewinn je Aktie konservativ gewählt wird z.B. ein Mittelwert der letzten 3-5 Jahre und dass dieser Gewinn nicht durch Sondereffekte verfälscht ist.
Die Formel neigt dazu sehr hohe werte auszuspucken wenn die Wachstumsraten seht hoch sind, hier sollte man die 2g auf 1,5 oder sogar auf 1 reduzieren.
Auch interessant:
>> Kurs-Gewinn-Verhältnis berechnen
>> Überblick der Englischen Börsenbegriffe
Werbung
Links* Meine Links sind Empfehlungslinks (Affiliate) die mit Amazon, Financeads oder Digistore24 verknüpft sind, wenn Du durch eines dieser Links auf Amazon etwas kaufst, bekomme ich eine kleine Werbevergütung, dadurch entstehen dir keine zusätzlichen Kosten, durch den Link unterstützt du meine Arbeit, hier schon mal vielen Dank an Dich.